Case Study and Meta-Analysis of the Use of Virtual Manipulatives

Mikyung Shin (Assistant Professor, West Texas A&M University)

Jiyeon Park (Assistant Professor, Eastern Kentucky University)

Kimberly Seale (Special Education Teacher, Model Lab School)

Contact: mikyung.shin@wtamu.edu

Slides: https://mshin77.github.io/2023CLD

Source: https://github.com/mshin77/2023CLD

Agenda

• Math Wall: Using Visual Representations

• What Are Virtual Manipulatives?

• Examples and Benefits of Virtual Manipulatives

• Resources for Selecting Educational Technology Tools

• Case Study on Synchronous Online Instruction

• Meta-Analysis: Three-Level Multilevel Modeling for Single-Case Data

Math Wall: Using Visual Representations

Source: Number Corner (Bridges Math)

What Are Virtual Manipulatives?

• A dynamic visual model operational in environments like the web.

• Initially developed through Flash or Java Applet programs in 1990s.

• Adaptable in various forms for extension, transformation, and selection.

• Can be employed for conceptual understanding in teaching and learning mathematics.

• Offers interactive opportunities for diverse mathematical learning.

• HTML5 was released in its public version in January 2008.

• With the introduction of HTML5 web standards, became available on mobile devices.

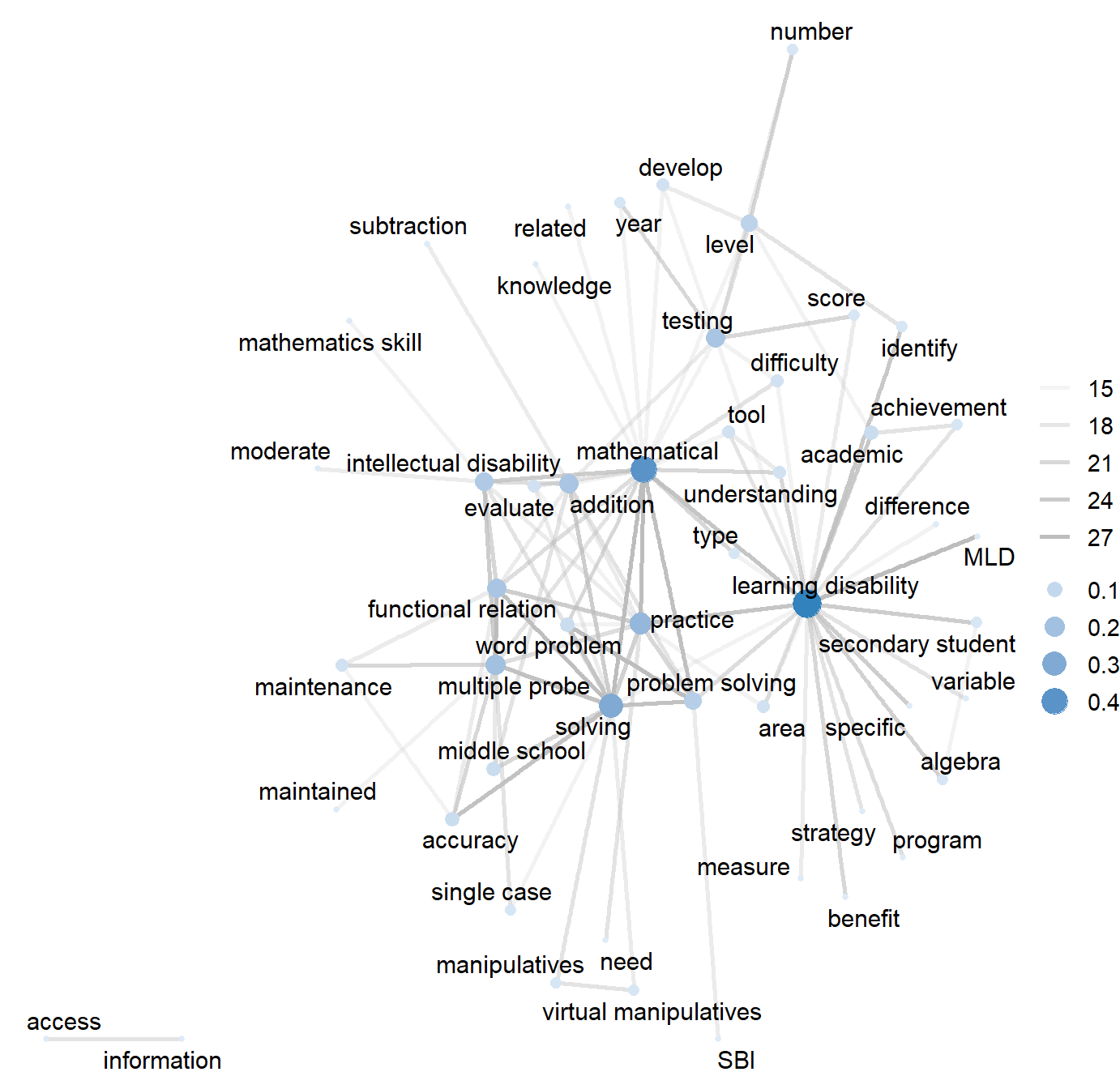
Word Networks Analysis

Source: Shin et al. (2023, p. 12)

• Since the 2010s, publications on the use of virtual manipulatives have increased.
• Incorporated within problem-solving instruction or an instructional sequence, such as virtual-representational-abstract (Bouck et al.,

Examples of Virtual Manipulatives

Source: Shin et al. (2023, p. 201)

Benefits of Virtual Manipulatives

• Content-specific visual models for targeted mathematics concepts and skills
• Feedback for students to facilitate memory retention
• Free and ready-to-use online materials
• Multiple opportunities for practice
• Integration with other online tools (e.g., digital games, augmented reality, virtual reality)

Source: GeoGebra

Augmented Reality - Overlay on the physical learning environment

Resources for Selecting Educational Technology Tools

Source: Common Sense Education

Case Study on Synchronous Online Instruction

Source: Park et al., (2023)

• Three fifth-grade students with learning disabilities

• Employing a multiple probe across participants single-case design

• 15 fraction lessons via video conferencing programs

Key Lesson Features and Results

• Lessons on Equivalent Fractions, Adapted from MSTAR Interventions (The University of Texas at Austin, 2011)
• Use of digital materials (i.e., virtual manipulatives, interactive whiteboard, and online assessments)
• Explicit instructions (i.e., lesson sequence of Introduction, Demonstration, Guided Practice, Independent Practice, and Closure)

• Students’ performance improved as the intervention was introduced; however, the extent and maintenance of improvement varied according to the students’ participation.

Park et al. (2023, p. 7)

Meta-Analysis: Three-Level Multilevel Modeling for Single-Case Data

Source: Shin et al. (2021)

• 35 studies published since 2000 on the effects of using virtual manipulatives for students with disabilities

• Case-level variables: grade and disability

• Study-level variables: pre-training purpose, Instructional method, type of virtual manipulative, Visual model

Multilevel Data Structure

• Single-case design data are hierarchically structured and can be displayed using three-level multilevel modeling (Baek et al., 2022; Moeyaert et al., 2021; Pustejovsky & Ferron, 2017).

• The levels examine repeated measurement occasions (Level 1) nested within cases (Level 2) and cases nested within studies (Level 3).

• Applied a piecewise linear regression approach by separately modeling time trends in the baseline and intervention phases (Singer & Willett, 2003).

Level 1 equation

\[ \begin{aligned} Y_{i j k}=& \beta_{0 j k}+\beta_{1 j k} \text { Intervention }_{i j k} \\ &+\beta_{2 j k} \text { Time }_{i j k}^{\prime} \times \text { Intervention }_{i j k}+e_{i j k}\\ & \text { with } e_{i j k} \sim N\left(0, \Sigma_e\right) \end{aligned} \]

\(y_{i j k}\) = mathematical accuracy at the measurement occasion, \(i\) th \((I=0,1, \ldots I)\), for the \(j\)th case\((j=1,2, \ldots J)\) in study \(k\); \(\beta_{0 j k}\) = baseline level; \(\beta_{1 j k}\) = change in level when the intervention phase starts (immediate effect); \(\beta_{2 j k}\) = change in slope between the baseline and the intervention phase; and \(e_{i j k}\) is an error term that is assumed to be independent and is normally distributed with a mean of 0 and variance of \(\sigma^2\).

• Random effects of immediate outcomes and trends during the use of virtual manipulatives were examined across various cases and studies.

• The interactions between each intervention effect and its moderating variables were investigated.

Key Findings

• Both the average immediate effect and trend during the intervention were statistically significant.
• The average immediate effect varied significantly by student grade, disability type, developer, device, type of virtual manipulative, and visual model embedded in virtual manipulatives.
• Neither student characteristics nor intervention feature–related moderators significantly influenced the average trend during the use of virtual manipulatives.
• Deviations in the moderation effects corroborate the need to examine trends during the use of virtual manipulatives, even after the immediate effects have been observed (Shin et al., 2021, p. 431)

Conclusion and Future Directions

• The methodology for identifying evidence of interventions can vary based on research design and purpose.
• Visual analysis of graphical data is necessary to validate the functional relationship and intervention effects in the case study.
• Moderation effects can be further examined through meta-analysis of single-case design data or studies.